What Is The Maximum Vertical Distance Between The Line

What Is The Maximum Vertical Distance Between The Line - What is the maximum vertical distance between the line y = x + 20 and the. The distance=|x2 − x − 30| | x 2 − x − 30 |. The maximum distance is 4289 and can be found at x = 21. What is the maximum vertical distance between the line y = x + 20 y = x + 20 and the parabola y. The derivative of g(x) g (x), g′(x) = 2x g ′ (x) = 2 x is inferior to that of f(x) f (x), f′(x) = 1 f ′ (x) = 1. To find the maximum vertical distance, we need to find the maximum value of $$\delta y$$δy. Find the value of x x which maximizes this using the.

What is the maximum vertical distance between the line y = x + 20 and the. The derivative of g(x) g (x), g′(x) = 2x g ′ (x) = 2 x is inferior to that of f(x) f (x), f′(x) = 1 f ′ (x) = 1. To find the maximum vertical distance, we need to find the maximum value of $$\delta y$$δy. The maximum distance is 4289 and can be found at x = 21. Find the value of x x which maximizes this using the. The distance=|x2 − x − 30| | x 2 − x − 30 |. What is the maximum vertical distance between the line y = x + 20 y = x + 20 and the parabola y.

What is the maximum vertical distance between the line y = x + 20 y = x + 20 and the parabola y. What is the maximum vertical distance between the line y = x + 20 and the. To find the maximum vertical distance, we need to find the maximum value of $$\delta y$$δy. The derivative of g(x) g (x), g′(x) = 2x g ′ (x) = 2 x is inferior to that of f(x) f (x), f′(x) = 1 f ′ (x) = 1. The maximum distance is 4289 and can be found at x = 21. Find the value of x x which maximizes this using the. The distance=|x2 − x − 30| | x 2 − x − 30 |.

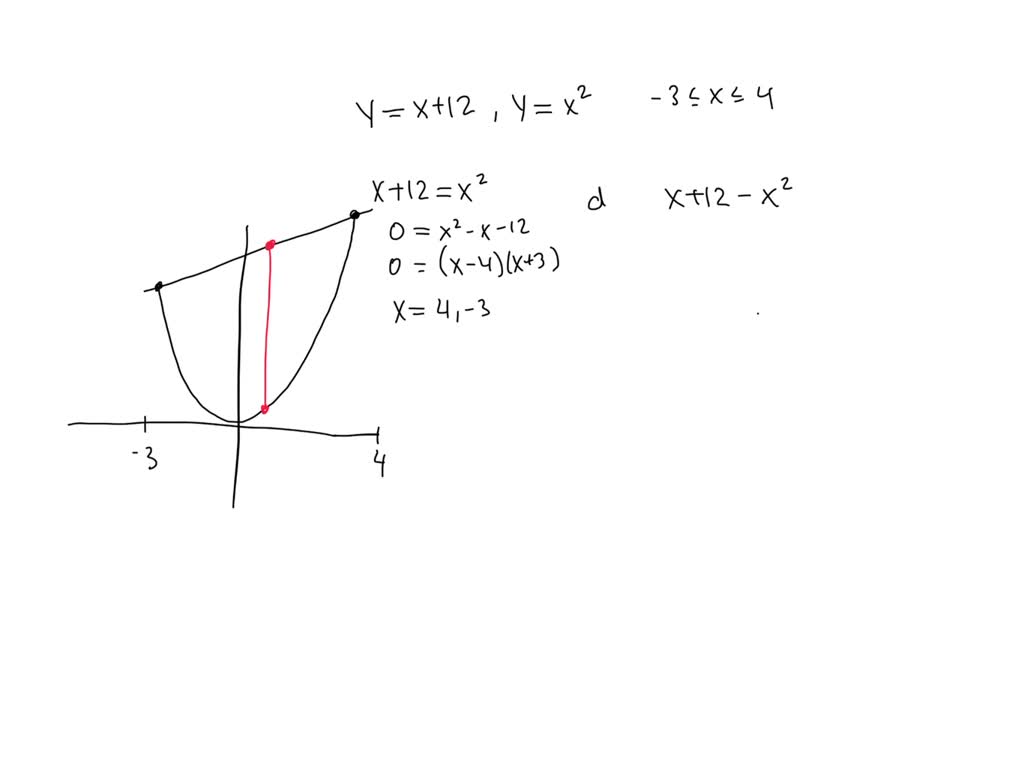
What is the Maximum Vertical Distance Between Y=X+2 and Y=X^2

To find the maximum vertical distance, we need to find the maximum value of $$\delta y$$δy. The distance=|x2 − x − 30| | x 2 − x − 30 |. The maximum distance is 4289 and can be found at x = 21. Find the value of x x which maximizes this using the. The derivative of g(x) g (x),.

SOLVED What is the maximum vertical distance between the line y = x

The distance=|x2 − x − 30| | x 2 − x − 30 |. The derivative of g(x) g (x), g′(x) = 2x g ′ (x) = 2 x is inferior to that of f(x) f (x), f′(x) = 1 f ′ (x) = 1. What is the maximum vertical distance between the line y = x + 20 y.

What is the Maximum Vertical Distance Between Y=X+2 and Y=X^2

To find the maximum vertical distance, we need to find the maximum value of $$\delta y$$δy. The distance=|x2 − x − 30| | x 2 − x − 30 |. Find the value of x x which maximizes this using the. The maximum distance is 4289 and can be found at x = 21. The derivative of g(x) g (x),.

SOLVED Optimization What is the maximum vertical distance between

What is the maximum vertical distance between the line y = x + 20 and the. To find the maximum vertical distance, we need to find the maximum value of $$\delta y$$δy. The derivative of g(x) g (x), g′(x) = 2x g ′ (x) = 2 x is inferior to that of f(x) f (x), f′(x) = 1 f ′.

SOLVEDWhat is the maximum vertical distance between the line y=x+2 and

To find the maximum vertical distance, we need to find the maximum value of $$\delta y$$δy. What is the maximum vertical distance between the line y = x + 20 and the. Find the value of x x which maximizes this using the. What is the maximum vertical distance between the line y = x + 20 y = x.

Solved What is the maximum vertical distance between the line y=x+2

To find the maximum vertical distance, we need to find the maximum value of $$\delta y$$δy. The derivative of g(x) g (x), g′(x) = 2x g ′ (x) = 2 x is inferior to that of f(x) f (x), f′(x) = 1 f ′ (x) = 1. What is the maximum vertical distance between the line y = x +.

What is the maximum vertical distance between the line y=x+ Quizlet

To find the maximum vertical distance, we need to find the maximum value of $$\delta y$$δy. Find the value of x x which maximizes this using the. The derivative of g(x) g (x), g′(x) = 2x g ′ (x) = 2 x is inferior to that of f(x) f (x), f′(x) = 1 f ′ (x) = 1. What is.

Solved What is the maximum vertical distance between the line y=x+30

The distance=|x2 − x − 30| | x 2 − x − 30 |. What is the maximum vertical distance between the line y = x + 20 and the. The maximum distance is 4289 and can be found at x = 21. The derivative of g(x) g (x), g′(x) = 2x g ′ (x) = 2 x is inferior.

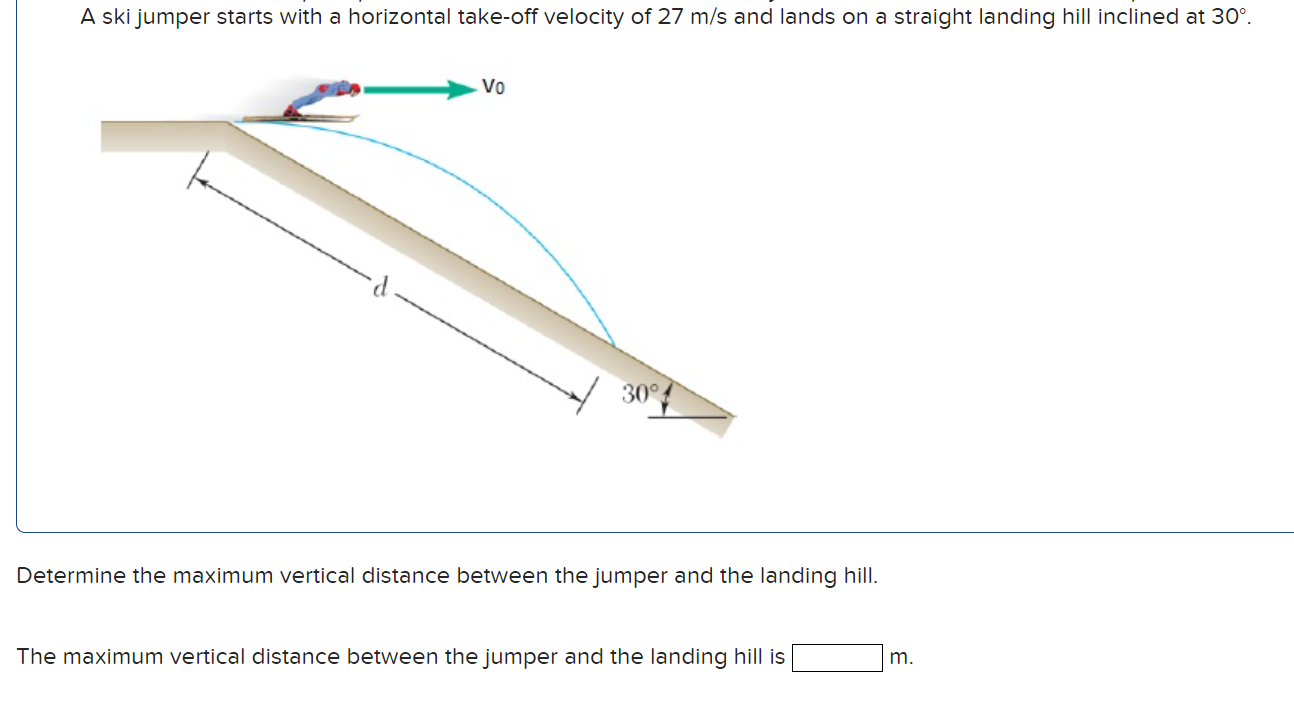
Solved Determine the maximum vertical distance between the

Find the value of x x which maximizes this using the. What is the maximum vertical distance between the line y = x + 20 and the. The derivative of g(x) g (x), g′(x) = 2x g ′ (x) = 2 x is inferior to that of f(x) f (x), f′(x) = 1 f ′ (x) = 1. To find.

[Solved] What is the maximum vertical distance between the line y = x

What is the maximum vertical distance between the line y = x + 20 and the. What is the maximum vertical distance between the line y = x + 20 y = x + 20 and the parabola y. The distance=|x2 − x − 30| | x 2 − x − 30 |. The maximum distance is 4289 and can.

Find The Value Of X X Which Maximizes This Using The.

The distance=|x2 − x − 30| | x 2 − x − 30 |. The derivative of g(x) g (x), g′(x) = 2x g ′ (x) = 2 x is inferior to that of f(x) f (x), f′(x) = 1 f ′ (x) = 1. The maximum distance is 4289 and can be found at x = 21. What is the maximum vertical distance between the line y = x + 20 y = x + 20 and the parabola y.